Potentials of Multitenancy Fine-Tuned LLM Serving

As open-source pre-trained Large Language Models (LLMs) become more powerful and permissive, more and more users are incorporating LLMs into their projects. An essential adaptation step is the integration of domain-specific documents into the pre-trained model, known as fine-tuning.

Often, the additional knowledge from domain-specific documents is minuscule compared to what the pre-trained model already knows. In such scenarios, the Low-Rank Adaptation (LoRA) technique proves valuable.

With LoRA, a fine-tuned model adds fewer than 0.1% of parameters to the pre-trained model. In concrete terms, this means a LoRA fine-tuned model increases storage by only 10~200 MB, depending on the configuration. From a computational standpoint, given the marginal increase in parameters compared to the pre-trained model, the additional computational load is relatively small.

Considering the minimal storage addition and computational overhead, I believe there’s potential in developing a multitenancy fine-tuned LLM serving service. This service could host thousands of LoRA models, all sharing the same backbone LLM. With batching, each user request would invoke a distinct fine-tuned model, thereby amortizing storage and computational costs across various models.

In my previous blog post, I delved into the batching effects in LLM serving. In this post, I’ll detail why multitenancy LoRA serving has immense potential.

Background: Text Generation

Text generation services like ChatGPT accept user text input and provide text responses. This input is referred to as a prompt. Internally, when an LLM processes text, it operates on a sequence of tokens. You can roughly think of a token as a few characters or a word. The text generation procedure has two primary phases:

• The Prefill phase (or “encode”, “init”) accepts the entire prompt and generates the subsequent token along with a KV cache.
• The Decode phase processes the newly created token and the KV cache then produces the following token while updating the KV cache. This phase repeats until the LLM completes its output.

Interestingly, even though the prefill phase handles 100x more tokens than the decode phase, their computational latencies are comparable. As the decode phase is repetitive, I’ll concentrate on its optimization in this post.

Background: LLM Architecture and Batching

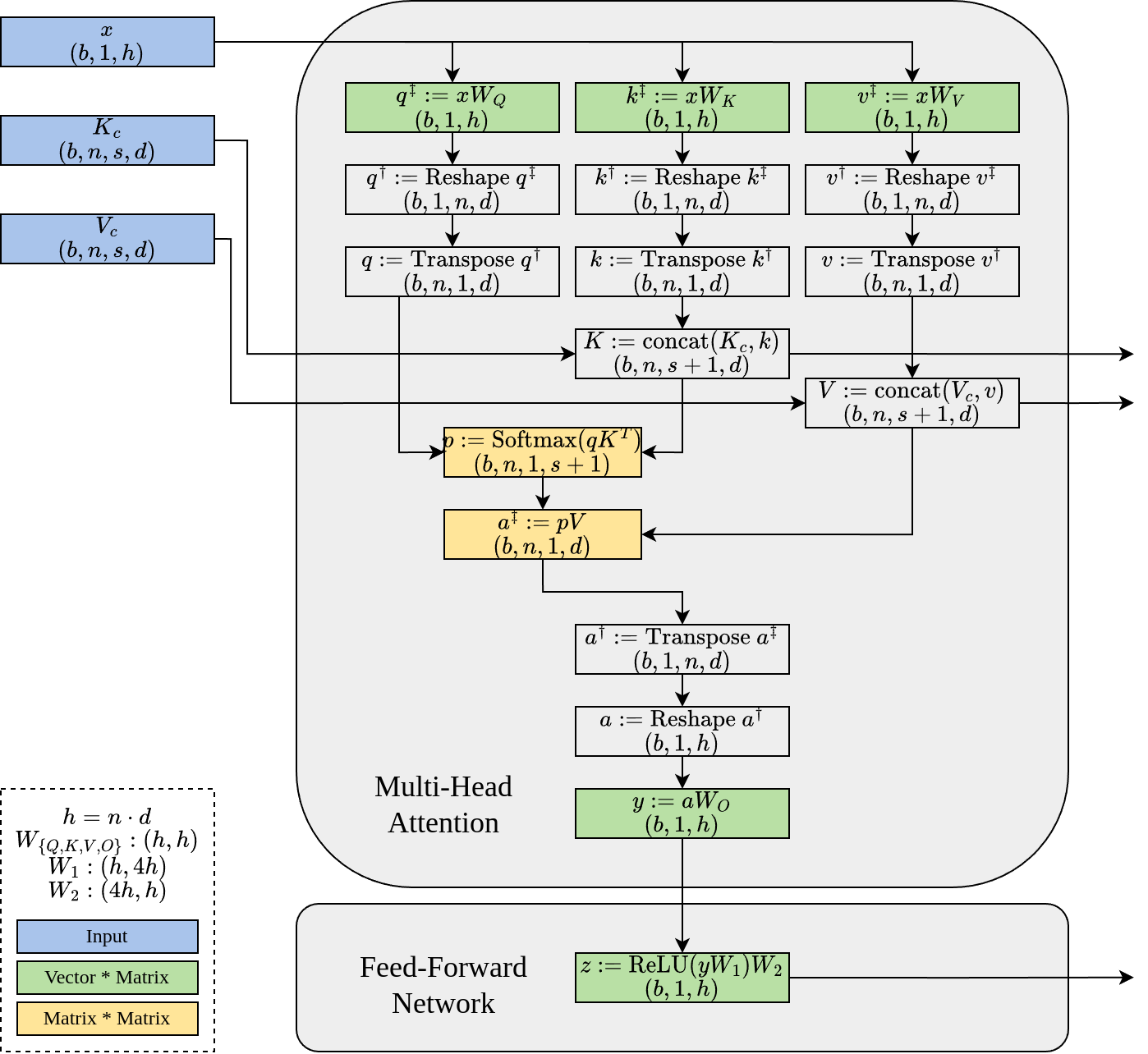
At its core, the LLM architecture is straightforward. It predominantly comprises multiple Transformer Layers, all sharing a uniform architecture. Each layer includes four compute-intensive components: QKV projection, self-attention, output projection, and a Feed-Forward Network (FFN).

Broadly, there are two primary operators:

• Self-Attention (highlighted in yellow) involves matrix-matrix multiplication.
• Dense Projection (highlighted in green) engages in vector-matrix multiplication.

Given that the input has a single token for each sequence in the batch, the dense projection computation is minuscule, too limited to make the most of a GPU. Therefore, expanding the batch size barely affects the latency of dense projections, making a large batch size essential for high-efficiency, low-latency serving.

For a more comprehensive analysis on LLM inference batching, check out my previous blog post.

Background: LoRA

Given a pre-trained weight W of shape [H1, H2], LoRA fine-tuning trains two small matrices, A of shape [H1, R], and B of shape [R, H2]. We use (W+AB) as the fine-tuned model weight. Here R is the rank, usually much smaller (around 8~32) than the original dimension (>= 4096).

The logic behind this approach is that the additional knowledge is fractional compared to the original weight, and hence, LoRA condenses the delta into two low-rank matrices.

LoRA’s drastically reduces the storage and memory requirements of a fine-tuned model in comparison to full fine-tuning.

In LLMs, as all parameters lie in the dense projections, LoRA can be integrated anywhere within the transformer layer. While the HuggingFace PEFT library introduces LoRA to q_proj and v_proj only, some studies like QLoRA advocate for its inclusion in all projections.

LoRA Latency and Batching Effect

Despite LoRA matrices being significantly smaller than the original weight matrix in storage terms, latency doesn’t decrease proportionately. We can benchmark the latency of the backbone model and the LoRA addon with the following code:

h1 = 4096
h2 = 11008
r = 16
for bs in range(1, 33):
  w = torch.randn(h1, h2, dtype=torch.float16, device="cuda:0")
  a = torch.randn(bs, h1, r, dtype=torch.float16, device="cuda:0")
  b = torch.randn(bs, r, h2, dtype=torch.float16, device="cuda:0")
  x = torch.randn(bs, 1, h1, dtype=torch.float16, device="cuda:0")
  bench(lambda: x @ w)
  bench(lambda: x @ a @ b)

The above figure indicates that the LoRA addon is merely 2.5x faster than the backbone model.

However, it’s evident that the LoRA batching effect mirrors that of the backbone model. An increase in batch size only marginally affects latency. This trait makes multitenancy LoRA exceptionally viable.

Unlike a standalone backbone LLM where all batch requests target the same model, in the context of multitenancy LoRA serving, batch requests might invoke different LoRA fine-tuned models. Expressed mathematically:

The challenge lies in applying corresponding LoRA addons to individual inputs within a batch while maintaining the “free lunch”-like batching effect.

Batched LoRA Operator

The batched LoRA operator we’re focusing on has this signature:

def add_lora(
    y: torch.Tensor,      # (batch_size, 1, out_features)
    x: torch.Tensor,      # (batch_size, 1, in_features)
    A: torch.Tensor,      # (num_loras, in_features, lora_rank)
    B: torch.Tensor,      # (num_loras, lora_rank, out_features)
    I: torch.LongTensor,  # (batch_size,)
):
  """Semantics: y[i] += x[i] @ A[I[i]] @ B[I[i]]"""
  raise NotImplementedError()

Naively, we can have a for-loop implementation over the batch dimension:

def lora_loop(
    y: torch.Tensor,  # (batch_size, 1, out_features)
    x: torch.Tensor,  # (batch_size, 1, in_features)
    A: torch.Tensor,  # (num_loras, in_features, lora_rank)
    B: torch.Tensor,  # (num_loras, lora_rank, out_features)
    I: torch.LongTensor,  # (batch_size,)
):
  for i, idx in enumerate(I.cpu().numpy()):
    y[i] += x[i] @ A[idx] @ B[idx]

Let’s benchmark the for-loop version. To give a point of comparison, we can include a “cheat” implementation where we assume the LoRA matrices for each request in the batch are already grouped together. This way, we only measure the latency of the batched matrix multiplication (bmm).

def lora_cheat_bmm(
    y: torch.Tensor,  # (batch_size, 1, out_features)
    x: torch.Tensor,  # (batch_size, 1, in_features)
    cheat_A: torch.Tensor,  # (batch_size, in_features, lora_rank)
    cheat_B: torch.Tensor,  # (batch_size, lora_rank, out_features)
):
  y += x @ cheat_A @ cheat_B


num_loras = 50
h1 = 4096
h2 = 11008
r = 16
A = torch.randn(num_loras, h1, r, dtype=torch.float16, device="cuda:0")
B = torch.randn(num_loras, r, h2, dtype=torch.float16, device="cuda:0")
for bs in range(1, 33):
  x = torch.randn(bs, 1, h1, dtype=torch.float16, device="cuda:0")
  y = torch.randn(bs, 1, h2, dtype=torch.float16, device="cuda:0")
  I = torch.randint(num_loras, (bs,), dtype=torch.long, device="cuda:0")
  cheat_A = A[I, :, :]
  cheat_B = B[I, :, :]

  bench(lambda: lora_loop(y, x, A, B, I))
  bench(lambda: lora_cheat_bmm(y, x, cheat_A, cheat_B))

Predictably, the for-loop version is significantly slower and loses the batching effect. This is because it processes inputs one by one, rather than leveraging the efficient CUDA kernels designed for batched data.

However, the bmm cheat approach offered an insight. The goal became clear: first gather all LoRA matrices into a temporary tensor, then use bmm. After some digging, I discovered the torch.index_select() function. It efficiently performs batched gathering, which led me to devise the gbmm (gather-bmm) implementation:

def lora_gbmm(
    y: torch.Tensor,  # (batch_size, 1, out_features)
    x: torch.Tensor,  # (batch_size, 1, in_features)
    A: torch.Tensor,  # (num_loras, in_features, lora_rank)
    B: torch.Tensor,  # (num_loras, lora_rank, out_features)
    I: torch.LongTensor,  # (batch_size,)
):
  a = torch.index_select(A, 0, I) # (batch_size, in_features, lora_rank)
  b = torch.index_select(B, 0, I) # (batch_size, lora_rank, out_features)
  y += x @ a @ b

BGMV Operator

While gbmm is effective, it’s not the ultimate solution. There’s no need to consolidate the LoRA addons into one contiguous space solely for bmm. Ideally, the aggregation could occur within the CUDA kernel as bmm operates. If possible, this would eliminate the GPU memory read and write operations associated with torch.index_select().

I turned to my friend Zihao Ye for help, who is an expert in crafting high-performance CUDA kernels. After a few iterations, Zihao developed an impressively fast CUDA kernel that accomplishes half of what LoRA requires. We’ve named this operator Batched Gather Matrix-Vector Multiplication (BGMV):

Subsequently, the add_lora() function can be realized using two BGMV calls:

def lora_bgmv(
    y: torch.Tensor,  # (batch_size, 1, out_features)
    x: torch.Tensor,  # (batch_size, 1, in_features)
    A: torch.Tensor,  # (num_loras, in_features, lora_rank)
    B: torch.Tensor,  # (num_loras, lora_rank, out_features)
    I: torch.LongTensor,  # (batch_size,)
):
  tmp = torch.zeros((x.size(0), A.size(-1)), dtype=x.dtype, device=x.device)
  bgmv(tmp, x, A, I)
  bgmv(y, tmp, B, I)

Here are the benchmark results for both gbmm and bgmv:

As the data shows, gbmm is commendably effective. The gathering process adds roughly 20% latency compared to bmm, but maintains a satisfactory batching effect. Impressively, bgmv outperforms even bmm, thanks to Zihao’s meticulous kernel work.

Multitenancy LoRA Text Generation Performance

Leveraging the bgmv kernel, I developed a research prototype named Punica that supports multiple LoRA models. It has the unique ability to batch requests for different LoRA models into a single model invocation. I benchmarked Punica against renowned systems like HuggingFace Transformers, DeepSpeed, Faster Transformer, and vLLM.

In the tests, each request targets a distinct LoRA model. Given that the other systems aren’t explicitly optimized for multitenancy LoRA serving, they operate with a batch size of 1. LoRA was integrated into HuggingFace Transformers and DeepSpeed using the HuggingFace PEFT library. I haven’t adjusted vLLM and Faster Transformer yet, so they ran without LoRA. Here are the results:

Thanks to optimized Transformer implementations, systems like DeepSpeed, vLLM, and Faster Transformers achieve 3x throughput compared to the standard HuggingFace Transformers. But since the batch size is capped at 1, they fall short in multitenancy LoRA serving efficiency.

Conversely, Punica boasts an 8x throughput at batch size 16 compared to these systems and a staggering 23x when stacked against vanilla HuggingFace Transformers. Notably, Punica’s throughput scales nearly linearly with increased batch sizes.

It’s worth noting that Punica is still an early-stage research prototype. It currently uses the same Transformer implementation as vanilla HuggingFace Transformers, with the exception of the LoRA and self-attention operators. Several known kernel optimizations for Transformer layers aren’t yet implemented in Punica yet, which justifies the performance disparity between it and other optimized systems at batch size 1.

But how does it fare in terms of latency?

As depicted, batching in Punica doesn’t introduce significant latency.

Example Use Cases

Having demonstrated the efficiency of multitenancy LoRA serving, let’s envision some potential applications:

• Fine-tuning a LoRA model on a fresh novel to aid readers in summarizing each character’s journey.
• Adapting a LoRA model to rapidly unfolding news to keep readers abreast of developments.
• Refining a LoRA model based on a webpage’s content, enhancing comprehension for readers.

I call this approach Just-in-time Fine-tuning due to LoRA’s fast training time. (In my trials, it’s under one second per epoch.)

Summary

This post showcased the feasibility of serving multiple fine-tuned LoRA models in batches. Punica, my prototype, exhibits almost linear throughput scaling without incurring latency penalties.

Check out Punica’s open-source code on Github: https://github.com/punica-ai/punica

You can access the benchmark code used in this post in this Jupyter notebook.

This research remains a work in progress. I’m actively working on this research project and I expect to release an online demo very soon. I welcome any feedback or thoughts – feel free to share in the comment section or via the buttons below.